2.1 向量的概念,操作和优越性
R使用各种类型的向量 (vector)来存储单一类型的数据。
2.1.1 创建向量(赋值)
单元素的向量,可以直接像这样赋值:
x <- 2
x#> [1] 2要创建一个多元素的向量,需要用到c() (concatenate)函数:
nums <- c(1,45,78)
cities <- c("Zürich", "上海", "Tehrān")
nums#> [1] 1 45 78cities#> [1] "Zürich" "上海" "Tehrān"通过length()函数,可以查看向量的长度。
length(nums)#> [1] 3#如果无后续使用,没必要赋值一个变量;c(...)的计算结果就是一个向量,并直接传给`length()`函数
length(c("Guten Morgen")) #> [1] 1(每个被引号包围的一串字符,都只算做一个元素,因此长度为1;多元素的向量请看第2.1.1节)
还是通过c()函数,可以把多个向量拼接成一个大向量:
cities_1 <- c("Zürich", "上海", "Tehrān")
cities_2 <- c("大阪", "Poznań", "Cairo")
cities <- c(cities_1, cities_2, c("Jyväskylä", "邯郸", "札幌่"))
cities#> [1] "Zürich" "上海" "Tehrān" "大阪" "Poznań" "Cairo"
#> [7] "Jyväskylä" "邯郸" "札幌่"2.1.2 索引/取子集/子集重新赋值 (indexing/subsetting)
索引 (index)就是一个元素在向量中的位置。R是从1开始索引的,即索引为1的元素是第一个元素(因此用熟了Python和C可能会有些不适应)。在向量后方使用方括号进行取子集运算(即抓取索引为对应数字的元素)。
x <- c("one", "two", "three", "four", "five", "six", "seven", "eight", "nine")
x[3]#> [1] "three"可以在方括号中使用另一个向量抓取多个元素:
x[c(2,5,9)] # 第2个,第5个,第9个元素#> [1] "two" "five" "nine"如果方括号内是一个负数向量:
x[-c(2,5,9)] # 除了第2个,第5个,第9个以外的元素#> [1] "one" "three" "four" "six" "seven" "eight"我们可以重新赋值子集:
x[c(2,5,9)] <- c("二", "五", "九")
x#> [1] "one" "二" "three" "four" "五" "six" "seven" "eight" "九"经常,我们会抓取几个连续的元素。如果想知道方法,请继续往下看。
2.1.3 生成器
有时候我们需要其元素按一定规律排列的向量,这时,相对于一个个手动输入,有更方便的方法:
2.1.3.1 连续整数
1:10 #从左边的数(包含)到右边的数(包含),即1:10#> [1] 1 2 3 4 5 6 7 8 9 10这时,你应该会有个大胆的想法:
x[3:6]#> [1] "three" "four" "五" "six"没错就是这么用的,而且极为常用。
当元素比较多的时候:
y <- 7:103
y#> [1] 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
#> [18] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
#> [35] 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
#> [52] 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
#> [69] 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
#> [86] 92 93 94 95 96 97 98 99 100 101 102 103注意到了左边方括号中的数字了吗?它们正是所对应的那一行第一个元素的索引。
下面的内容可能有点偏,可以酌情从这里跳到第2.1.5节。
2.1.3.2 复读机rep()
rep(6, 8) # 把6重复8遍;或rep(6, times = 8)#> [1] 6 6 6 6 6 6 6 6rep(c(0, 7, 6, 1), 4) # 把(0, 7, 6, 1)重复4遍#> [1] 0 7 6 1 0 7 6 1 0 7 6 1 0 7 6 1rep(c(0, 7, 6, 1), each = 4) # 把0, 7, 6, 1各重复4遍#> [1] 0 0 0 0 7 7 7 7 6 6 6 6 1 1 1 1rep(c(0, 7, 6, 1), c(1, 2, 3, 4)) # 把0, 7, 6, 1分别重复1, 2, 3, 4遍#> [1] 0 7 7 6 6 6 1 1 1 1想一想,rep(8:15, rep(1:5, rep(1:2, 2:3)))的计算结果是什么?
2.1.3.3 等差数列: seq()
公差确定时:
seq(0, 15, 2.5) # 其实是`seq(from = 0, to = 50, by = 5)`的简写#> [1] 0.0 2.5 5.0 7.5 10.0 12.5 15.0长度确定时:
seq(0, 50, length.out = 11) # 其实是`seq(from = 0, to = 50, length.out = 11)`的简写#> [1] 0 5 10 15 20 25 30 35 40 45 502.1.3.4 随机数:
连续型均匀分布随机数用runif(n, min, max),n是数量,min是最小值,max是最大值。默认min为0,max为1。
x_unif <- runif(100000, 40, 60) # 生成100000个40到60之间,连续均匀分布的的随机数
hist(x_unif) # 画直方图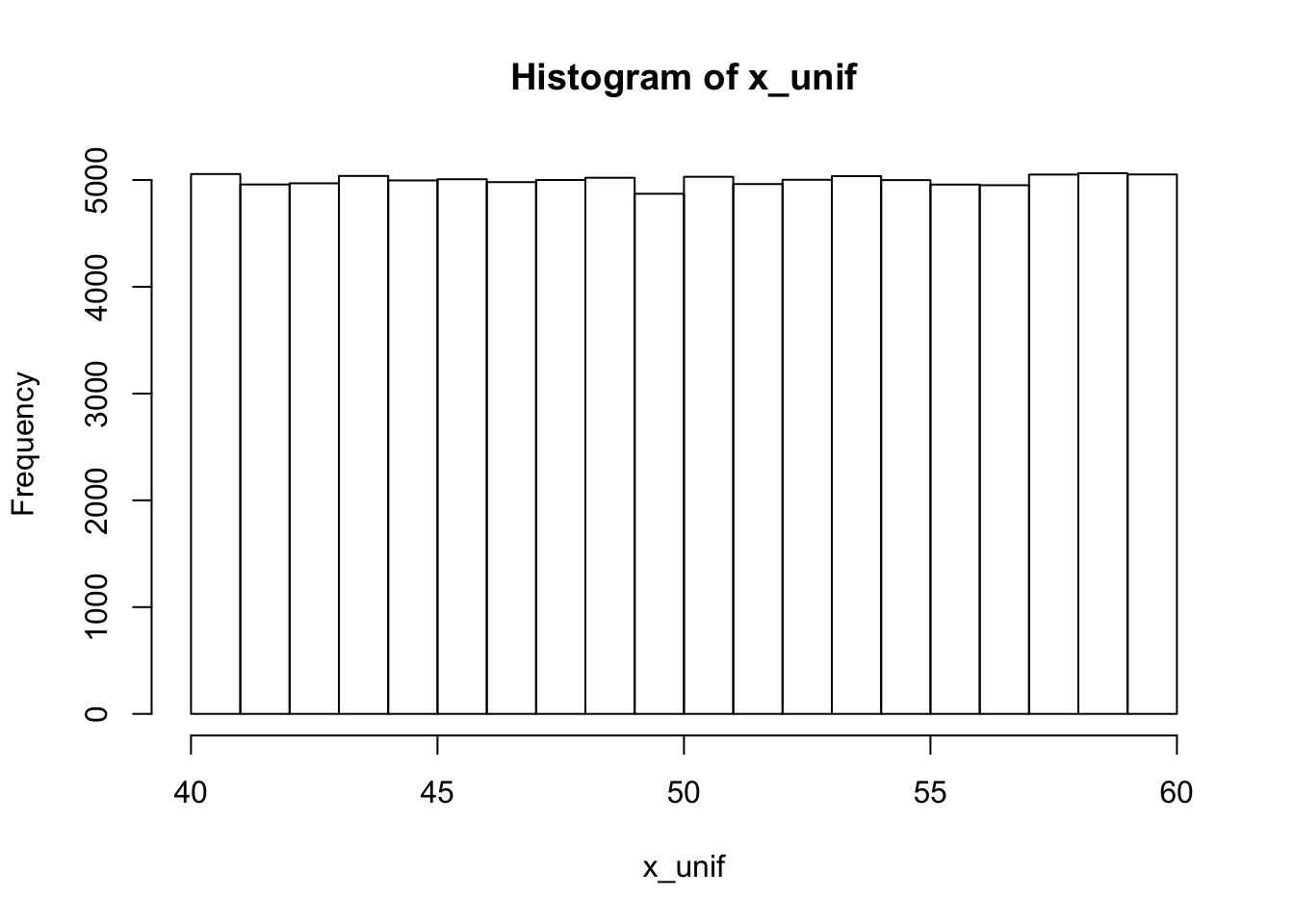
正态分布随机数用rnorm(n, mean, sd), 三个参数分别为数量,平均值,标准差。默认mean为0,sd为1。
x_norm <- rnorm(100000, 250, 20) # 按照平均值为250,标准差为20的正态分布的概率密度函数生成100000个随机数
hist(x_norm) # 画直方图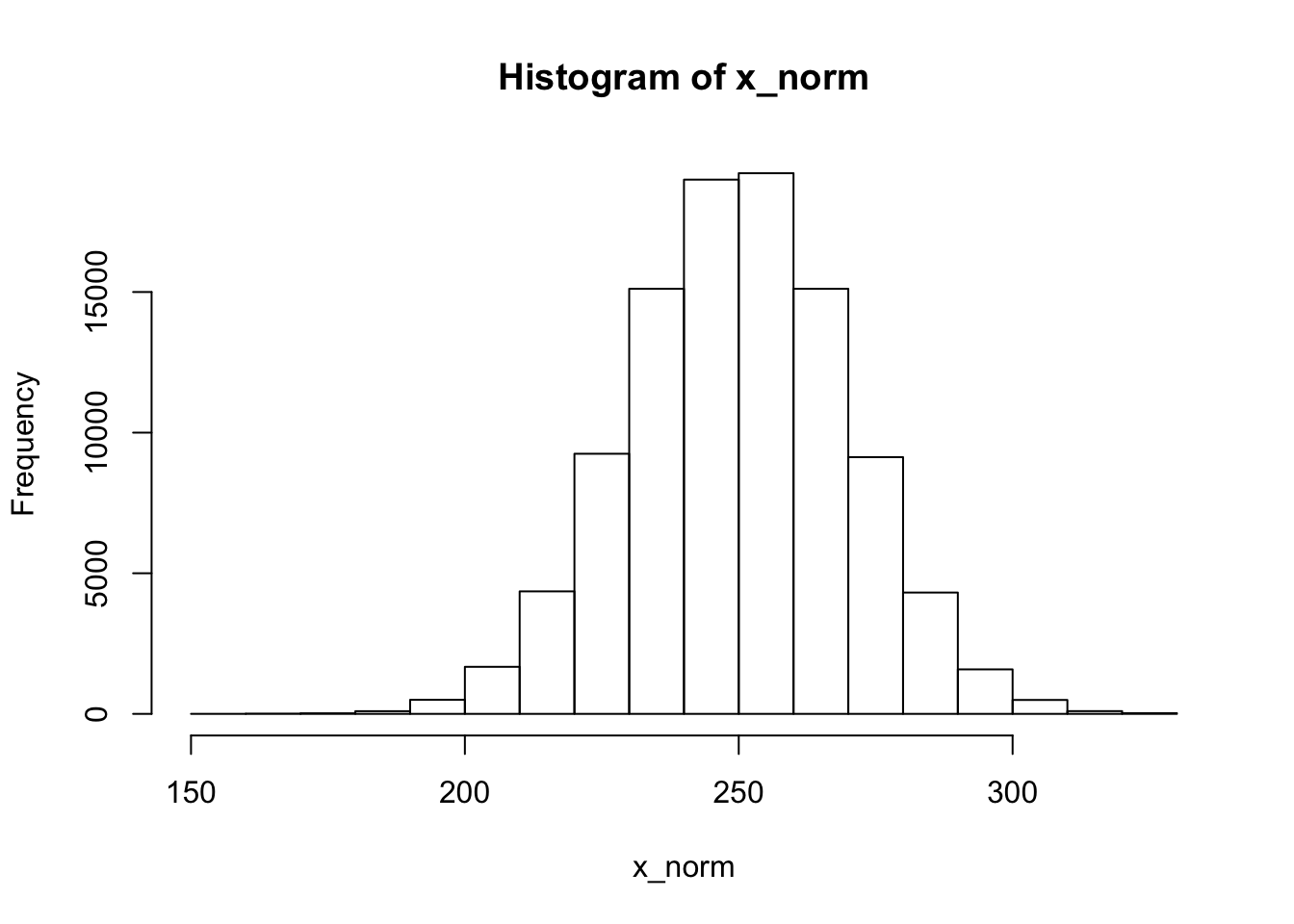
此外,还有rlnorm(), rpois(), rexp()等函数。?stats::distributions中介绍了R中自带的分布,其中大部分都有对应的随机数生成器。
2.1.3.5 简单随机抽样
随机抽样的应用比随机数要广。
假设一个盒子里有10个球,上面分别写着字母“a”至“j”.
balls <- letters[1:10]
balls#> [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j"我想从这10个球中随机取20个球,每取一次之后,把球放回去:
sample(balls, 20, replace = TRUE)#> [1] "a" "d" "f" "h" "b" "e" "h" "f" "d" "e" "a" "g" "f" "j" "d" "g" "c"
#> [18] "f" "j" "i"我想从这10个球中随机取3个球,取完之后不把球放回去:
sample(balls, 3) # 即`sample(balls, 3, replace = FALSE)`#> [1] "c" "e" "d"可以看到,sample()函数第一个参数是样本空间,第二个参数是样本量。
当然,它经常被用作随机整数生成器(这也是我为什么把它放在这一小节):
sample(1:100, 10, replace = TRUE)#> [1] 38 23 28 22 67 82 10 74 33 22在后面的章节中,比如第3.3.1.4节,我们会学到sample()更实际的用法。
2.1.4 向量的其他操作
2.1.4.1 创建长度为0的向量
使用循环的时候,经常需要初始化一个长度为0的向量(见第2.7节
有两种方法实现:
x <- vector("numeric")
# 或`vector("integer")`, `vector("character")`等
class(x)#> [1] "numeric"或者:
x <- integer(0)
# 或 x <- integer()
# 或`character(0)`, `numeric(0)`等
class(x)#> [1] "integer"其中后面这种方法亦可用于创建长度为\(n\)的向量,把0替换成你想要的长度即可。
2.1.4.2 sort(), rank()和order()
x <- c(2, 5, 3, 6, 10, 9, 7, 8, 1, 4)
sort(x)
rank(x)
order(x)
rev(sort(x))
# 为方便同框展示,我用的代码是 list(x = x), `sort(x)` = sort(x), `rank(x)` = rank(x), `order(x)` = order(x), `rev(sort(x))` = rev(sort(x)))#> $x
#> [1] -10 5 -89 999 84
#>
#> $`sort(x)`
#> [1] -89 -10 5 84 999
#>
#> $`rank(x)`
#> [1] 2 3 1 5 4
#>
#> $`order(x)`
#> [1] 3 1 2 5 4
#>
#> $`rev(sort(x))`
#> [1] 999 84 5 -10 -89sort()很好理解,就是把原向量的元素从小到大重新排列。如果要从小到大:rev(sort(x)).
rank()是原向量各个元素的(从小到大的)排名。(-10是第2名,5是第3名,-89是第1名,以此类推)
order()是一个原向量索引的排序,使得x[order(x)] = sort(x),即x[order(x)] = x[c(3, 1, 2, 5, 4)] = c(-89, -10, 5, 84, 999) = sort(x)
至于文字向量,英文按a, b, c, d, e, ...排列,中文按笔画排列。15
2.1.4.3 元素的命名
scores <- c(ochem = 79, math = 66, mcb = 64, blc = 75, bpc = 72)
scores#> ochem math mcb blc bpc
#> 79 66 64 75 72然后便可以额外地用名字抓取元素:
scores[c("math", "bpc")] == scores[c(2, 5)]#> math bpc
#> TRUE TRUE2.1.4.4 unique()函数
unique()函数用来列举一个向量中所含的,不重复的元素,比如:
unique(c("a", "a", "x", "x", "x", "b", "h", "h"))
#> [1] "a" "x" "b" "h"2.1.5 R向量的优越性
R中的向量(矩阵和数列也是)的各种计算默认都是逐元素 (elementwise)的。比如:
x <- c(4, 9, 25)
y <- c(8, 6, 3)
x + y#> [1] 12 15 28x * y # 在matlab中这样乘是不行的,要用`.*`,除法也是#> [1] 32 54 75sqrt(x)#> [1] 2 3 5拥有这种特性的计算也被称为向量化计算 (vectorized computation).
相比于常用的编程语言,向量化计算省去了for循环,计算效率得到极大的提升;相比于matlab的默认矩阵乘法,逐元素乘法在数据处理中更有用。
若想更多地了解向量化计算(比如如何使用apply()族函数把for循环需要39秒的运算压缩到0.001秒),请看第2.7.4节。
标点符号、特殊字符也有固定的排列顺序,通过这串代码查看常用符号的排列顺序:
sort(strsplit("`~!@#$%^&*()_+-=[]\\{}|:;'\",./<>?", "")[[1]])↩