2.3 数学表达和运算
2.3.1 数的表达
2.3.1.1 浮点数
除非指定作为整数(见下),在R中所有的数都被存储为双精度浮点数的格式 (double-precision floating-point format),其class为numeric。
class(3)#> [1] "numeric"这会导致一些有趣的现象,比如\((\sqrt{3})^2 \neq 3\):(强迫症患者浑身难受)
sqrt(3)^2-3#> [1] -4.44e-16浮点数的计算比精确数的计算快很多。如果你是第一次接触浮点数,可能会觉得它不可靠,其实不然。在绝大多数情况下,牺牲的这一点点精度并不会影响计算结果(我们的结果所需要的有效数字一般不会超过10位;只有当两个非常,非常大且数值相近对数字相减才会出现较大的误差)。
作为R版版主,应该做到在凌晨四点突然被人叫醒问你10乘以0.1等于几,你在1秒钟之内斩钉截铁回答,不是1!
——谢益辉19
2.3.1.2 科学计数法
在R中可以使用科学计数法(AeB\(= A \times 10^B\)),比如:
3.1e5#> [1] 310000-1.2e-4+1.1e-5#> [1] -0.0001092.3.1.3 整数
整数的class为integer。有两种常见的方法创建整数:
1)在数后面加上L;
class(2)#> [1] "numeric"class(2L)#> [1] "integer"2)创建数列
1:10 #公差为1的整数向量生成器,包含最小值和最大值#> [1] 1 2 3 4 5 6 7 8 9 10class(1:10)#> [1] "integer"seq(5,50,5) #自定义公差,首项,末项和公差可以不为整数#> [1] 5 10 15 20 25 30 35 40 45 50class(seq(5,50,5)) #因此产生的是一个浮点数向量#> [1] "numeric"seq(5L,50L,5L) #可以强制生成整数#> [1] 5 10 15 20 25 30 35 40 45 50class(seq(5L,50L,5L)) #是整数没错#> [1] "integer"整数最常见的用处是indexing(索引)。
2.3.1.3.1 整数变成浮点数的情况
这一小段讲的比较细,请酌情直接跳到下一节(2.3.2)。
整数与整数之前的加,减,乘,求整数商,和求余数计算会得到整数,其他的运算都会得到浮点数,(阶乘(factorial)也是,即便现实中不管怎么阶乘都不可能得到非整数):
class(2L+1L-5L%%3L)#> [1] "integer"class(4L*9L%/%5L)#> [1] "integer"class(1000L/1L)#> [1] "numeric"class(3L^4L)#> [1] "numeric"class(sqrt(4L))#> [1] "numeric"class(log(exp(5L)))#> [1] "numeric"class(factorial(5L))#> [1] "numeric"整数与浮点数之间的运算,显然,全部都会产生浮点数结果,无需举例。
2.3.2 运算
2.3.2.1 二元运算符号
R中常用的binary operators(二元运算符)有:
| 符号 | 描述 |
|---|---|
+ |
加 |
- |
减 |
* |
乘 |
/ |
除以 |
^或** |
乘幂 |
%/% |
求整数商,比如7%%3\(=2\) |
%% |
求余数,比如7%%3\(=1\) |
其中求余/求整数商最常见的两个用法是判定一个数的奇偶性,和时间,角度等单位的转换。(见本章小测)。
2.3.2.2 \(e^x\)和\(\log_x{y}\)
exp(x)便是运算\(e^x\)。如果想要\(e=2.71828...\)这个数:
exp(1)#> [1] 2.72log(x, base=y)便是运算\(\log_y{x}\),可以简写成log(x,y)(简写需要注意前后顺序,第2.8.2有解释)。
默认底数为\(e\):
log(exp(5))#> [1] 5有以10和2为底的快捷函数, log10()和log2()
log10(1000)#> [1] 3log2(128)#> [1] 72.3.2.3 近似数(取整,取小数位,取有效数字)
取有效数字用signif()函数;第一个参数是对象,第二个参数是保留的位数;若保留的位数未指定,默认为6.
signif(12.3456789, 4)#> [1] 12.3当对象的有效数字小于你想保留的有效数字位数时,它不会让你乱来(下面round()函数也类似):
signif(12.3, 8)#> [1] 12.3保留小数位用round()函数。
round(12.3456789, 3) # 保留3个小数位#> [1] 12.3若不指定保留多少位,默认为0,即四舍五入地取整:
round(13.5)#> [1] 14此外,还有三种取整函数:floor(), ceiling()和trunc()
floor(5.6) # = 5 # “地板”;比x小的最近的整数
ceiling(5.4) # = 6 # “天花板”;比x大的最近的整数
floor(-5.6) # = -6 # 不是-5,因为-6是比-5.6小的最近的整数
ceiling(-5.4) # = -5 # 不是-6;因为-5是比x大的最近的整数
trunc(-5.6) # = -5 # 你可能需要这个;它无视了小数点后面的位数注意,所有取整函数给出的的结果都并不是整数。如果你一定需要的话,可以用as.integer()函数把它转换成真·整数。
class(ceiling(7.4))#> [1] "numeric"2.3.2.4 NA, Inf, NaN相关
我不知道张三有几个苹果,我也不知道李四有几个苹果;你问我张三和李四共有几个苹果:
NA + NA#> [1] NA鬼才知道咧!
类似地,NA - NA, NA/NA, NA*NA, log(NA)都等于NA
NA^0等于几?别上当!R的开发者们可没有忘记\(\forall x\in \mathbb{R:x^0 = 1}\)
Inf, 即\(\infty\), 表示很大的数字(准确地说,大于等于\(2^{1024}\)即\(1.797693\times10^{308}\)的数字)它还有个负值,-Inf. 以下是几个结果为Inf的例子:
exp(1000) # = Inf; 这个很明显
1/0 # = Inf; 0被当作很小的数
0^(-1) # = 1/(0^1) = 1/0 = Inf
log(0) # = -Inf; 0又被当作很小的数NaN是“非数” (not a number). 运算结果为NaN的例子有:
0/0 # NaN
log(-1) # = NaN
0^(3+8i) # = NaN + NaNi
Inf-Inf; Inf/Inf # = NaN
-NaN # = NaNInf和NaN的类型是numeric(浮点数).
class(Inf); class(NaN)#> [1] "numeric"#> [1] "numeric"is.na()会判定NaN为真:
is.na(NaN)#> [1] TRUE2.3.2.5 R中自带的常用数学函数概览
| 函数 | 描述 |
|---|---|
exp(x) |
\(e^x\) |
log(x,y) |
\(\log_yx\) |
log(x) |
\(\ln(x)\) |
sqrt(x) |
\(\sqrt{x}\) |
factorial(x) |
\(x!=x\times(x-1)\times(x-2)\ldots\times2\times1\) |
choose(n,k) |
\(\binom{n}{k}=\frac{n!}{k!(n-k)!}\)(二项式系数) |
gamma(z) |
\(\Gamma(z)=\int_0^\infty x^{z-1}e^{-x}dx\)(伽马函数) |
lgamma(z) |
\(\ln(\Gamma(z))\) |
floor(x), ceiling(x), trunc(x), |
取整;见上一小节。 |
round(x, digits = n) |
四舍五入,保留n个小数位,n默认为0 |
signif(x,digits = n) |
四舍五入,保留n个有效数字,n默认为6) |
sin(x), cos(x), tan(x) |
三角函数 |
asin(x), acos(x), atan(x) |
反三角函数 |
sinh(x), cosh(x), tanh(x) |
双曲函数 |
abs(x) |
\(|x|\)(取绝对值) |
sum(...), prod(...) |
所有元素相加之和/相乘之积 |
2.3.3 简易的统计学计算
本节简要解释了R中的基础统计学函数,t分布,t检验和\(\chi^2\)检验。统计学方法并不是本书的重点,因此可以酌情跳到第2.6节(基础内容:逻辑)或第2.4节(进阶内容:列表)。
2.3.3.1 基础
中位数median(); 平均数mean(); 方差var(); 标准差sd().
2.3.3.2 t分布
众所周知,t分布长这样:
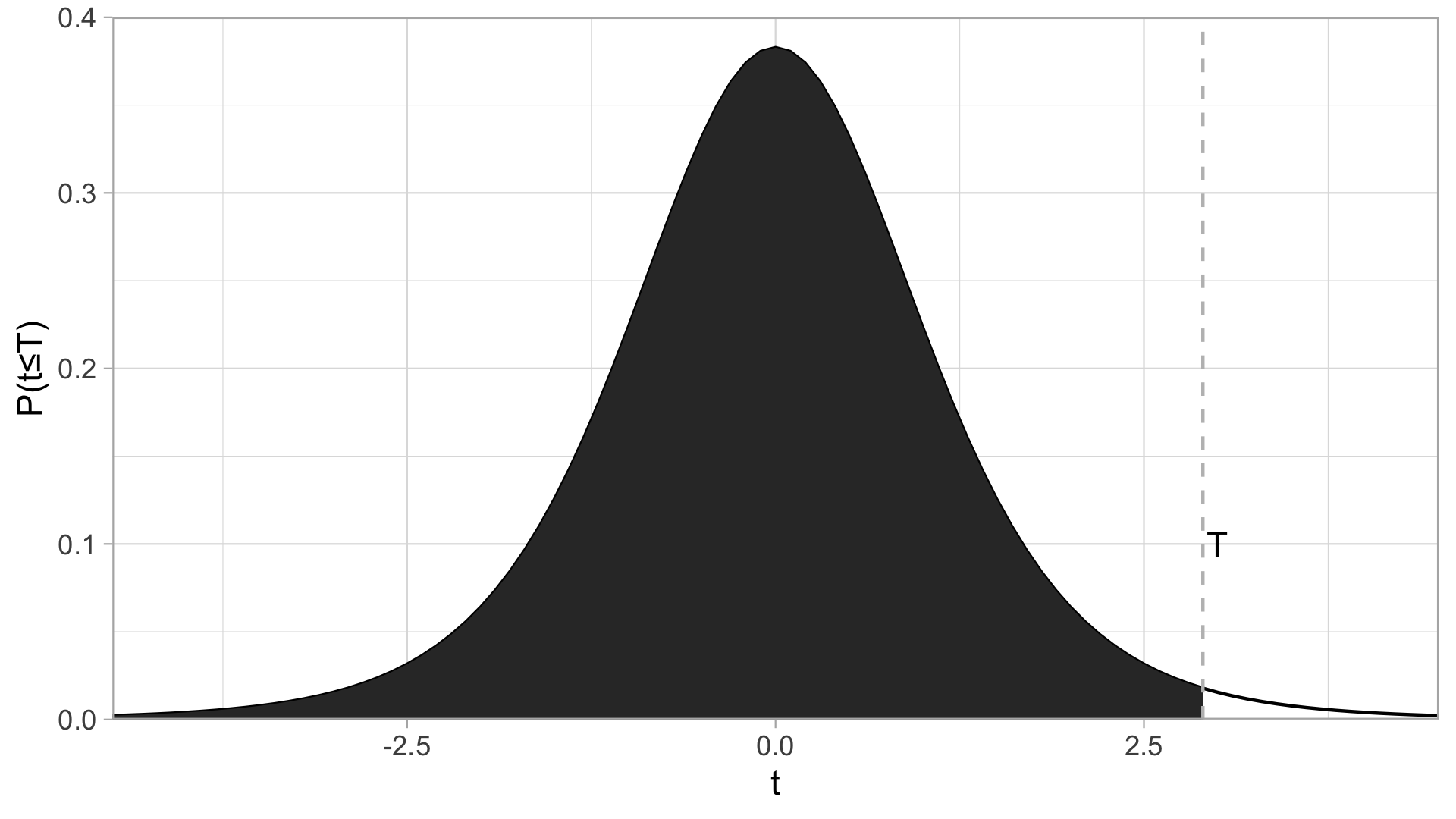
阴影面积为\(P(t<T)\),虚线对应的\(t\)为\(T\).
qt()可以把\(P(t≤T)\)的值转化成\(T\),pt()则相反。
假设你需要算一个confidence interval(置信区间),confidence level(置信等级)为\(95\%\),即\(\alpha=0.05\),degrees of freedom(自由度)为\(12\),那么怎么算\(t^*\)呢?
qt(0.975, df = 12)#> [1] 2.18为什么是\(0.975\)?因为你要把\(0.05\)分到左右两边,所对应的t*就等同于t分布中,\(P(t ≤ T) = 0.975\)时T的值。
再举一个例子,你在做t检验,双尾的,算出来\(t=1.345\),自由度是\(15\),那么\(p\)值怎么算呢?
p <- (1-(pt(2.2, df = 15)))*2
p#> [1] 0.0439其中pt(2.2, df = 15)算出阴影面积(\(P(t≤T)\)的值),1减去它再乘以2就是对应的双尾t检验的\(p\)值。
2.3.3.3 z分布
没有z分布专门的函数。可以直接用t分布代替,把df调到很大(比如999999)就行了。比如我们试一下\(95\%\)置信区间所对应的\(z*\):
qt(0.975,9999999)#> [1] 1.96(果然是\(1.96\))
2.3.3.4 t检验
t检验分为以下几种:
- One sample t test (单样本)
- paired t test(配对)
- Two sample…(双样本)
- Unequal variance (Welch) t test(不等方差)
- Equal variance t test(等方差)
在R中做t检验,很简单,以上这些t检验,都是用t.test 这个函数去完成。
以单样本为例:
x <- c(2.23,2.24,2.34,2.31,2.35,2.27,2.29,2.26,2.25,2.21,2.29,2.34,2.32)
t.test(x, mu = 2.31)#>
#> One Sample t-test
#>
#> data: x
#> t = -2, df = 10, p-value = 0.07
#> alternative hypothesis: true mean is not equal to 2.31
#> 95 percent confidence interval:
#> 2.26 2.31
#> sample estimates:
#> mean of x
#> 2.28可以看到\(p=0.06766\)。
R的默认是双尾检验,你也可以设置成单尾的:
x <- c(2.23,2.24,2.34,2.31,2.35,2.27,2.29,2.26,2.25,2.21,2.29,2.34,2.32)
t.test(x, mu = 2.31, alternative = "less") # 检验是否*less* than μ#>
#> One Sample t-test
#>
#> data: x
#> t = -2, df = 10, p-value = 0.03
#> alternative hypothesis: true mean is less than 2.31
#> 95 percent confidence interval:
#> -Inf 2.31
#> sample estimates:
#> mean of x
#> 2.28\(p\)值瞬间减半。
双样本/配对:
x <- c(2.23,2.24,2.34,2.31,2.35,2.27,2.29,2.26,2.25,2.21,2.29,2.34,2.32)
y <- c(2.27,2.29,2.37,2.38,2.39,2.25,2.39,2.16,2.55,2.81,2.19,2.44,2.22)
t.test(x, y)#>
#> Welch Two Sample t-test
#>
#> data: x and y
#> t = -2, df = 10, p-value = 0.1
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.1846 0.0292
#> sample estimates:
#> mean of x mean of y
#> 2.28 2.36R的默认是non-paired, unequal variance,你可以通过增加paired = TRUE,var.equal = TRUE这两个参数来改变它。
t.test(x, y, paired = TRUE)#>
#> Paired t-test
#>
#> data: x and y
#> t = -1, df = 10, p-value = 0.2
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.1925 0.0372
#> sample estimates:
#> mean of the differences
#> -0.07772.3.3.5 \(\chi^2\) 检验
\(\chi^2\)检验有两种,goodness of fit test(适配度检验)和contigency table test/test of independence(列联表分析/独立性检验)。都是用chisq.test()函数去完成。
2.3.3.5.1 适配度检验
假设我们制造了一个有问题的骰子,使1至6朝上的概率分别为:
expected_probs <- c(0.05, 0.1, 0.15, 0.2, 0.2, 0.3)然后我们投掷了100次,实际1至6朝上的次数分别为:
observed_vals <- c(6, 9, 14, 24, 18, 29)通过chisq.test(),检验实际的1至6朝上概率是否与预期有偏差:
chisq.test(observed_vals, p = expected_probs) # 参数p是指概率#>
#> Chi-squared test for given probabilities
#>
#> data: observed_vals
#> X-squared = 1, df = 5, p-value = 0.9p值很大(远大于0.05),因此结论是骰子各面朝上的概率符合预期。
如果不指定p参数,默认为检测是否所有值相等(即骰子的所有面朝上的概率相等):
chisq.test(observed_vals)#>
#> Chi-squared test for given probabilities
#>
#> data: observed_vals
#> X-squared = 20, df = 5, p-value = 3e-04这时p值小于0.05. 得出“骰子各面朝上的概率不等”的结论。
2.3.3.5.2 列联表分析/独立性检验
假设我们有一组不同年级的学生参加社团的人数数据:
(社团参与 <- matrix(c(28,36,40,40,32,33,38,29,36), nrow = 3, dimnames = list(c("一年级", "二年级", "三年级"), c("棒球", "足球", "网球"))))#> 棒球 足球 网球
#> 一年级 28 40 38
#> 二年级 36 32 29
#> 三年级 40 33 36我们想知道社团的参与,与所在年级是否是独立事件:
chisq.test(社团参与)#>
#> Pearson's Chi-squared test
#>
#> data: 社团参与
#> X-squared = 4, df = 4, p-value = 0.4p值不小于0.05,无法拒绝“社团的参与,与所在年级是独立事件”的虚无假设。
彩蛋:用R代码实现卡方分布的概率密度函数的图像:
#其实还可以更精简,但是为了易读性不得不牺牲一点精简度。
Z <- matrix(rep(rnorm(1000000), 6), nrow = 6)^2
X <- Z^2
Q <- matrix(nrow = 6, ncol = 1000000)
for (i in (1+1):6) {
Q[1,] = Z[1,]
Q[i,] = Q[(i-1),] + Z[i,]
}
plot(NULL, xlim=c(0.23,6), ylim = c(0,1),
main = expression(paste('X ~ ', chi^'2', '(k)')),
xlab = "x",
ylab= expression(f[k]*'(x)')
)
colors <- c('blue', 'black', 'red', 'green', 'gray', 'orange')
for (i in 1:6) {
lines(density(Q[i,]),
col=colors[i],
lwd=2)
}
legend('topright',c('k=1','k=2','k=3','k=4','k=5','k=6'),
fill = colors)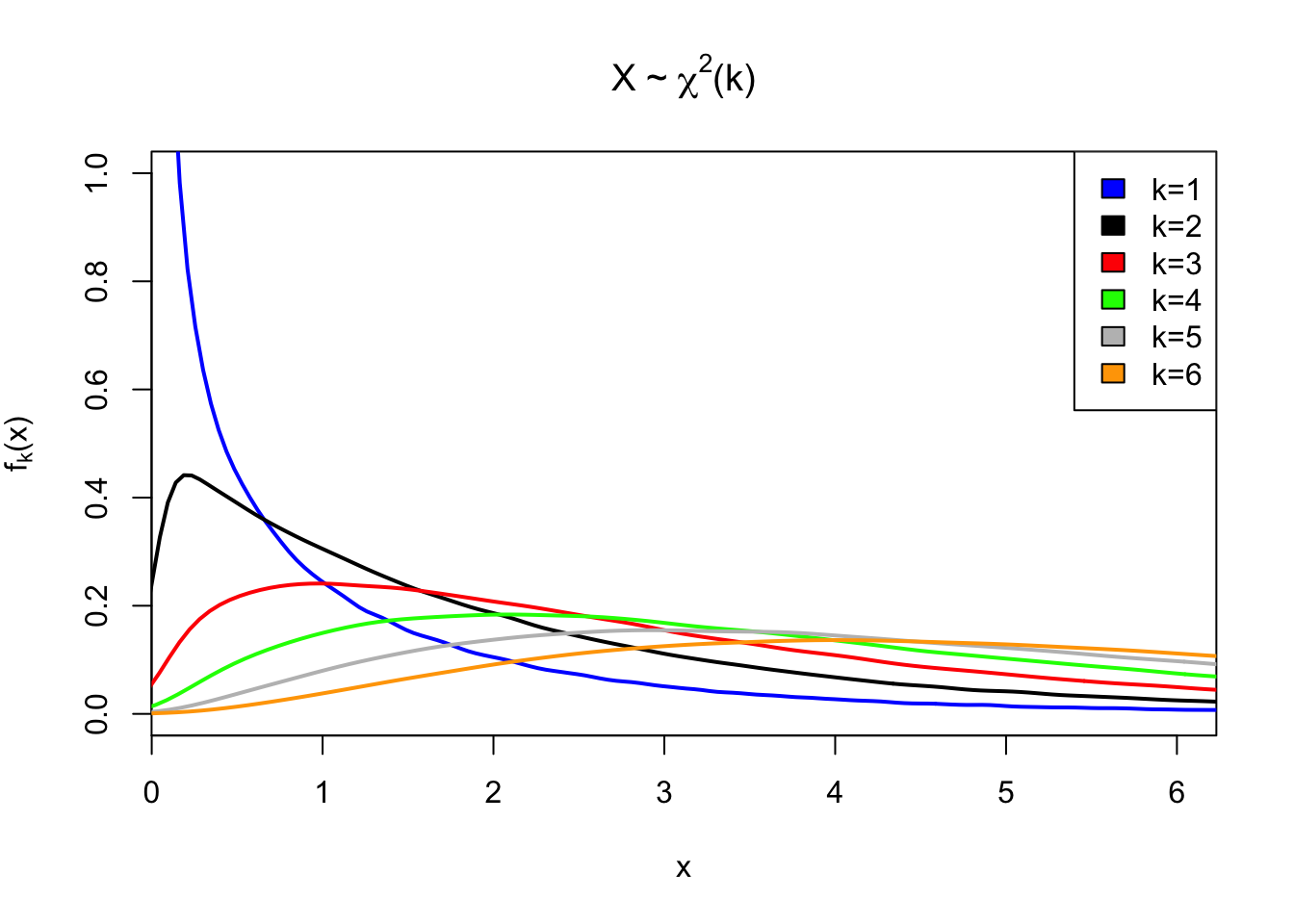
2.3.3.5.3 其他
R自带的检验还有Box.test(), PP.test(), ansari.test(), bartlett.test(), wilcox.test等共31种。查看帮助文件或利用网络资源以了解更多。
虽然,
0.1 * 10 - 1 == 0确实为TRUE.↩